While Andy was working on his own implementation of the genetic algorithm from my previous post, he ran across an interesting phenomena that speaks to the difficulty of Cartpole: his randomly initialized neural net would be beat benchmark a nontrivial amount of the time.

I wanted to explore this further because I found his results surprising. Cartpole is a fairly well known classic control benchmark and it seems valuable to understand the difficulty of this benchmark. Such et al. also had made reference to this effect:

These examples and the success of RS versus DQN, A3C, and ES suggest that many Atari games that seem hard based on the low performance of leading deep RL algorithms may not be as hard as we think, and instead that these algorithms for some reason are performing poorly on tasks that are actually quite easy.

So first I explored the performance of a completely random policy on CartPole-v1. If we just flip a coin to choose our action at each step, we get the following distribution of performance:

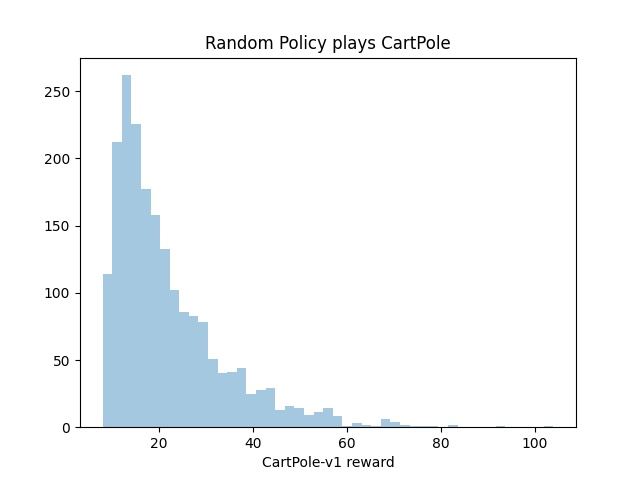
Random Policy on Cartpole

The bulk of the runs last between 10 and 30 steps. The best we do in 2000 trials is one game with a reward of 104.

So now I’ll random initialize a bunch of small neural nets (each with 4 densely connected ReLu neurons leading to a sigmoid output neuron) to play Cartpole:

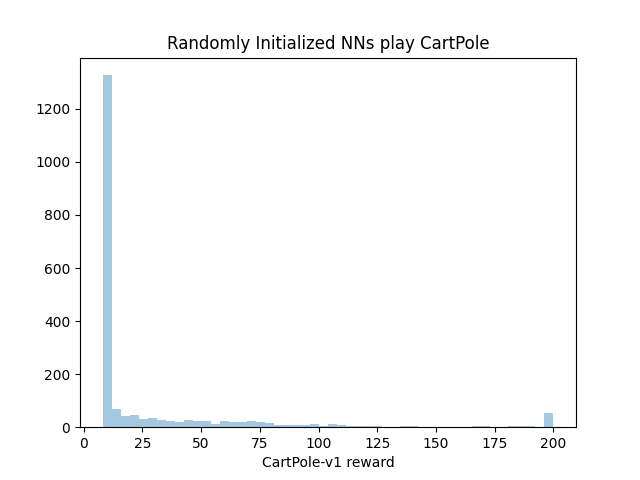
Random NN on Cartpole

Note that we do absolutely no training on these neural nets, we just play Cartpole using whatever weights keras generates on initialization. In this case, while the bulk of neural nets do not play Cartpole much better than random policies, there are a few that play perfect games right out of the box (50 out of 2000 trials or 2.5% of our nets).

We can also drop the neural nets that play poorly (that is, get a score of less than 15) to get a better look at the distribution of “competent” nets:

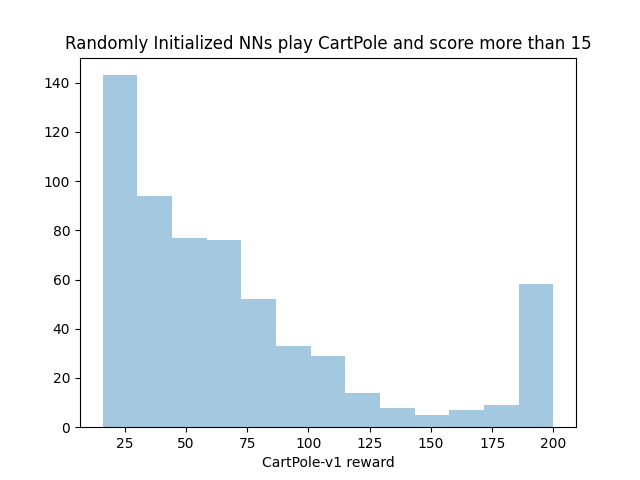
Competent NN on Cartpole

This looks quite a bit like a power law distribution with a collapsing of the long tail into the 200 reward category (because we cut off the benchmark at 200 steps, nets that could play for 250 and 1000 steps all end up in that last bucket).

So what does this mean? Realistically, Cartpole is more of a “hello world” than a serious benchmark people use to evaluate RL algorithms, so the particulars of these results don’t matter much. At a higher level, though, it’s interesting that:

  1. A randomly initialized neural net performs differently than a random coin flip. This implies that the particular function computed by a randomly initialized neural net of this architecture is different from a binomial function and more amenable to solving Cartpole.

  2. If you imagine all the policies that could be represented by a neural net of this architecture as a space, then that space will have a structure of good versus bad policies and this structure is potentially very relevant for how easy or difficult the benchmark is for that architecture.

  3. If you view training as how you move through the aforementioned policy space, then the particulars of your training algorithm and the structure of the policy space can interact to impact the difficulty of the benchmark.

Such et al. have more discussion along these lines and I’d recommend taking a look at their paper.

Check out my benchmarking code here.

Check out my raw results here.