Tabular Q-Learning for Cartpole

I mentioned in my previous post on genetic algorithms that I had been working on re-implementing some classic reinforcement learning algorithms and applying them to Cartpole. One of those algorithms was Q-Learning where Q-values are stored in a table (rather than the currently-more-popular deep neural nets).

Using tabular Q-learning only really makes sense if the state space isn’t huge or if you can quantize the state space in a way that doesn’t completely lose the structure of the problem. Put another way, you need to revisit states over different runs to be able to learn anything about them and act on those learnings.

If you can pull this off, though, then using tables eliminates a lot of debugging, hyperparameter optimization, and other baggage that using a general function approximator like a neural net brings along.

For Cartpole, the state is fully represented by four floating point numbers. Rounding each of those numbers to a 2 decimal fixed point seems to reduce the state space enough that learning can occur while keeping the table a manageable size.

The algorithm I implemented was taken from Sutton and Barto’s section on off policy TD control. Their pseudocode is below:

Results

I don’t think it’d be accurate to say that this implementation solved Cartpole, at least not as cleanly as the previously tested genetic algorithm. The results below are from running for ~6hrs on my mid-2012 MacBook Air:

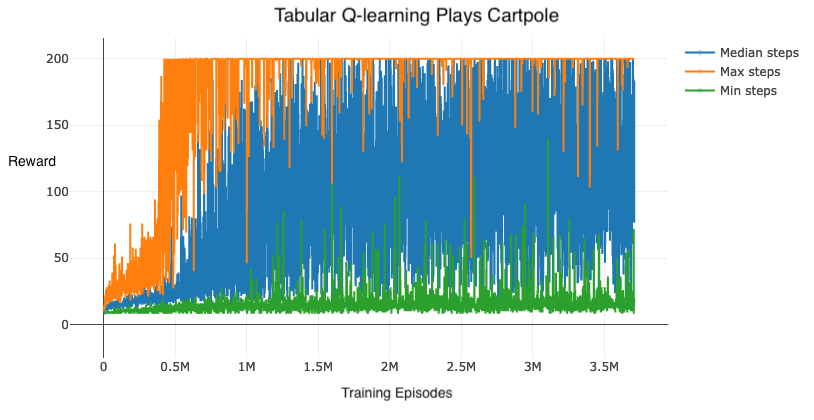
Each point in the above graph represents 10 completely on-policy rollouts (i.e. always take the action with the highest Q-value in a given state). You can see we relatively quickly train up to being able to sometimes beat Cartpole, but we still do miserably other times. Exploring whether this is just a symptom of a lack of training or if the state quantization is too coarse (or if there is some other issue) will be left to future work.

Check out my code here.