Running a Genetic Algorithm on Cartpole
I implemented a version of the genetic algorithm described in Such et al.’s Deep Neuroevolution paper and applied it to Cartpole. After futzing around with some policy gradient algorithms, I was pleasantly surprised how straightforward and effective the genetic algorithm implementation was on this benchmark.
Highlights of my implementation:
- I run the algorithm for up to 1000 generations (in practice, about 20 generations are sufficient for solving Cartpole).
- I start with 10 randomly-initialized, densely-connected sequential neural
nets. The architecture of each neural net is as follows:
- 4 input neurons
- A dense 16 neuron relu layer
- A dense 8 neuron relu layer
- A sigmoid output neuron which represents the probability of going left
- For each generation, I instantiate 90 child neural nets which have the weights of the fittest nets from the previous generation perturb by Gaussian noise. I also port forward the 10 best performing nets from the previous generation so each generation contains 100 nets.
- I evaluate each net in each generation on 10 runs of Cartpole, I take the mean reward of these 10 runs as the fitness of the net.
- I carry forward the 10 fittest nets to the next generation and instantiate new child nets from those fittest nets.
- I consider Cartpole solved when all 10 trials of the fittest nets result in a reward of 200.
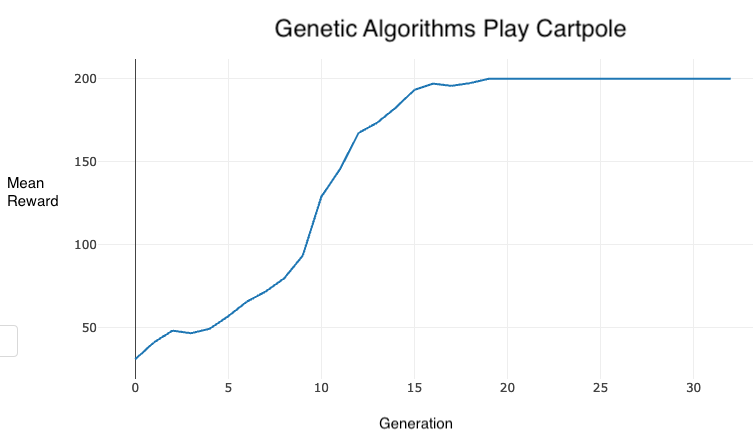
Results
My implementation solved Cartpole after 20 generation running for ~45min on a mid-2012 MacBook Air:
Check out my code here.
Check out my notes on the Such et al. paper here.
Note posted on
by Nick Jalbert